２つの同つの同心球導体の表面に異なる電位を設定し、導体間の単位長あたりの静電容量を電界解析ソフトウェアF-VOLTによる評価解析で求めました。
今回解析対象としました２つの同心球導体の外観は図１、２の通りです。
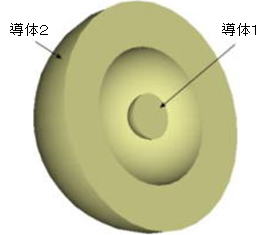 図１ ２つの導体の外観図(1/2断面図) |
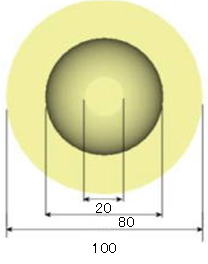 図２ ２つの導体の位置関係(単位：mm) |
静電容量を求めるための理論式は以下のようになります。
上記図１で、導体１の中心から電位面までの距離をa (図２では10mm)、導体２の中心から電位面までの距離をb（図２では30mm）とすると、その電位面間の静電量を求める計算式は次のようになります。
同心球の静電容量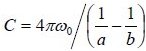
真空中の誘電率
軸対称形状になりますので、２次元軸対称メッシュモデルとしました。
電位設定条件として、下記図３のように、導体１の表面に電位１Ｖを、導体２の表面に0Ｖを設定しました
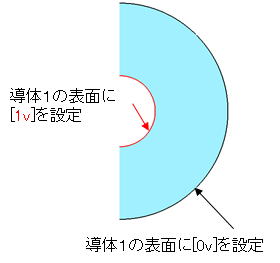
図３ 入力条件
解析結果、 F-VOLTでは、電荷総量(Q)が計算されます。
電荷総量Q ： 1.6755×10-12（C）
Q = CV (V=1.0 (V)より
静電容量C ： 1.6755 x 10-12（F） = 1.6755（pF）（F） = 50.638（pF）
また、上記理論式より、
静電容量(理論値) C ： 1.6689x10-12（F） = 1.6689（pF）
となり、解析結果値と理論式による計算結果値との誤差は、約0.4％となりました。
その他、電位分布と電界分布は以下のようになりました。
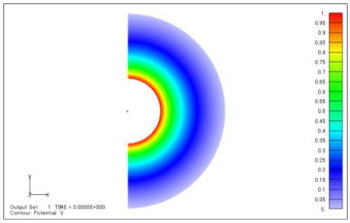 図４ 電位コンタ図(単位：V) |
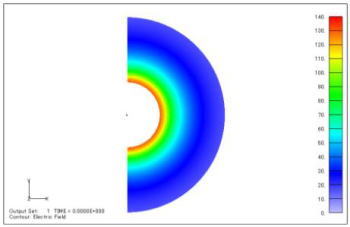 図５ 電界コンタ図(単位：V/m) |
 図６ 電界ベクトル分布(部分拡大図)(単位：V/m) |
この評価解析は電界解析ソフトウェア F-VOLT で行いました。
F-VOLT につきましてこちらへ
評価解析につきましてこちらへ
この解析結果につきまして詳細な内容をご希望の方は、資料請求ページの「ご質問／ご要望等」欄にその旨ご記入ください。
※各商標または商品名はそれぞれの所有権保持者の商標または登録商標です。