PHOTO-VOLTでは電場解析と電流分布解析ができます。
解析対象、必要な解析結果によりこれらを使い分ける必要があります。
電場解析の基礎方程式は、

です。

一方、電流分布解析の基礎方程式は

です。

電場解析は、基礎方程式からわかるように、時間変化が無いような定常状態の解析です。
一方、電流分布解析は、非定常な状態(変位電流の影響がある場合等)や定常的に電荷が移動する(電流が流れる)ような場合を対象としています(図１)。

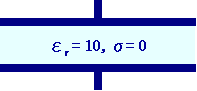電流が流れない場合（電場解析）
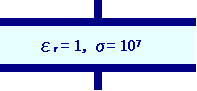定常電流が流れる場合<br> （電流分布解析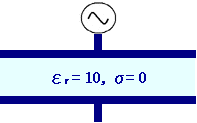）		交流が流れる場合<br> （電流分布解析）
＜図１＞

さらに進んで、電気抵抗は小さいが導体(銅や鉄)ほどではない場合、どうすればよいのでしょうか。

抵抗の大きな導体の中に電荷を密度ρで置いた場合、電荷は導体の中が同電位になるように、電流として流れて拡散します。

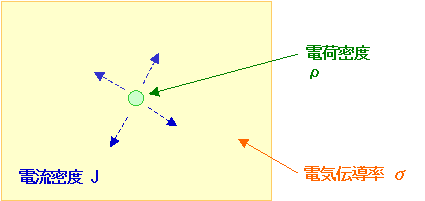
この電荷は、どのくらいの時間で拡散して流れてしまうのか、大体の所を見積もると、

電荷の連続の方程式
オームの法則
マクスウェルの方程式の1つ
および 式

から、一様な物質中で

が得られます。

これを解くと

となります。電荷密度が元の 1/e になる時間(時定数)は、

ここで、真空の誘電率 ε は 8.85 x 10^-12 なので、導体の電気伝導率を σ = 1.0 x 10⁷S/m 程度とすると、

τ = 8.85 x 10^-19(S)

となり、一瞬で電荷は拡散してしまいます。

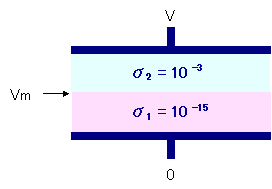
このことを踏まえて、図３のような導体としては抵抗が大きな物質がある系を考えると、時定数のオーダーは

程度となり、ナノ秒程度の時間変化を問題としない限り、Vm は V と同電位としてよいと言えます。