電流や電荷の受ける力は次のローレンツ力で計算できることはよく知られています。

　　 ・・・ （７）

ここにVは力を計算する電荷や電流が含まれている領域です。
ところで、誘電体や磁性体に働く力はこの式から計算できるのでしょうか。答えは明らかに否です。この式は、電荷と電流以外に関する力は含まれていませんので、それ以外の力を計算することはできません。
それでは、このような力を求めるにはどのようにすればよいのでしょうか。

　　 ・・・ （８）

が発生しますが、この電荷にも電場による力が働きます。また分極電流

　　 ・・・ （９）

や磁化電流

　　 ・・・ （１０）

も磁場によって通常の電流と同じように力を受けます。
このことの正当性は（４）式を、（５）式を使って書き直し

　　 ・・・ （１１）

や（３）式を（６）式を使って書き直した

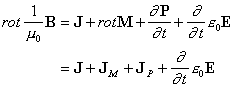　　 ・・・ （１２）

から、ρ_pが電荷と、またＪ_Ｍ、Ｊ_Ｐが電流と同様の役割を果たしていることを考えると納得することができます。このように考えると、誘電体や磁性体も含めた場合の電磁力は、（７）式を書き直した次の式で表現することができます。

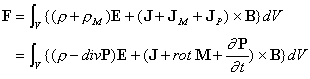　　 ・・・ （１３）

（３）、（４）、（５）、（６）式を使って書き直すとこの式は

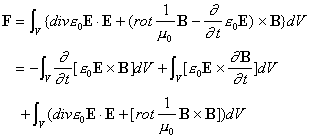
となります。この式を更に変形すると、次の成分式が得られます。

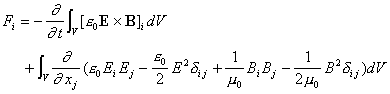　　 ・・・ （１４）

ここで次のテンソルを定義します。

　　 ・・・ （１５）

これより（１４）式は、

　　 ・・・ （１６）

この式はガウスの発散定理を使って次のようにも書けます。

　　 ・・・ （１７）

ただし、Sは領域V の境界面であり、n は領域V から外向きにとったSの単位法線ベクトルです。

これで、誘電体や磁性体も含めた電磁力の計算方法が得られました。
ここで定義されたテンソルT_{i j} はマックスウェルの応力テンソルと呼ばれています。
応力テンソルと呼ばれる理由は、（１６）式の右辺第二項が応力が物体に与える力と同じ形をしているからです。