誘導加熱による歯車の焼入れ

（比透磁率の温度依存性を考慮）

時間変動する電流を流し、歯車の発熱密度分布および温度分布を「PHOTO-EDDYjωとTHERMOの連成」で解析しました。 今回は比透磁率を、温度に依存する(強連成)場合と依存しない(弱連成)場合について解析を行いました。

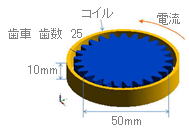図１　解析モデル外観図

これまで「PHOTO-EDDYjω」と「PHOTO-THERMO」による連成解析で比透磁率の温度依存性を考慮するためには、「PHOTO-THERMO」から出力された発熱ファイルデータを「PHOTO-EDDYjω」が読み込む必要がありましたが、「PHOTO-EDDYjωとTHERMOの連成」ではこのプロセスが自動化されましたので、発熱ファイルを介さずに自動で解析することができます。

図２　メッシュ図(全体)

今回解析しました解析モデルは、図３の通りです。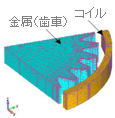

図３　メッシュ図(解析対象)

渦電流解析では、金属(歯車)の比透磁率の温度依存性を図４のように設定し、コイルには2000[A]／100[kHz]の電流を印加しました。 熱伝導解析では、渦電流解析により計算された発熱密度を荷重とし、0.25秒間隔で5秒間、20ステップの計算を行い、温度の時間的な変化を求めました。

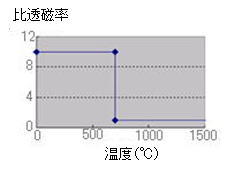図４ 比透磁率の温度依存性 （仮想的な物性値として います。）

解析結果は以下の通りです。

図５　磁束密度[T] 実部	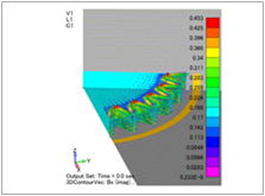図６　磁束密度[T] 虚部
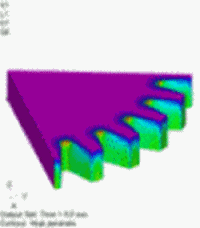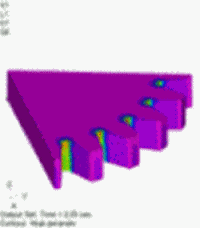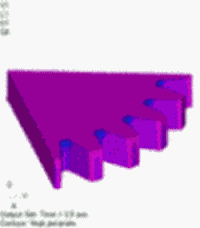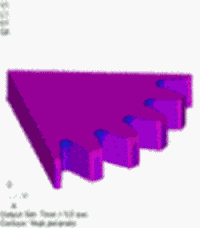図７　発熱密度分布[W/m3] 温度依存性あり(強連成)	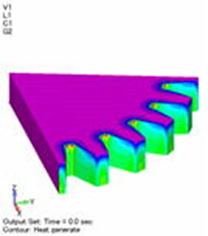図８　温度依存性なし(弱連成) *1
*1 最初に計算された発熱密度が最終ステップまで使用されます。

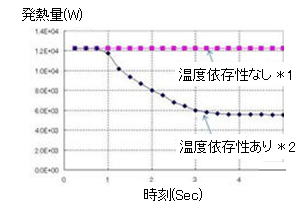
図９　発熱量[W]の時間変化

*1 ： 1ステップ目のみ発熱を計算
*2 ： 温度による比透磁率の変化が生じたときだけ発熱を計算しなおしています。
すべてのステップにおいて発熱を計算しているわけではありません。

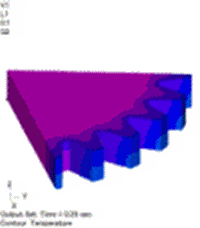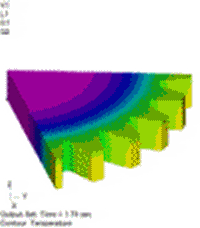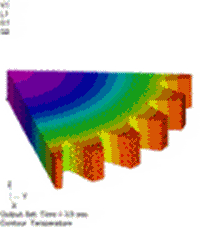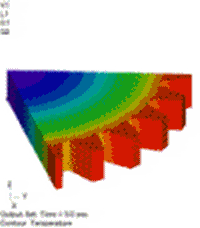図１０　温度分布[℃] 温度依存性あり（強連成）

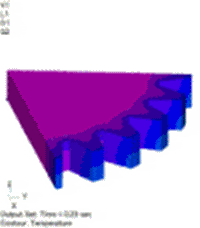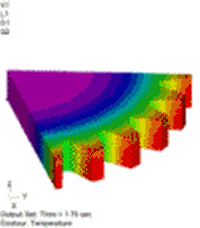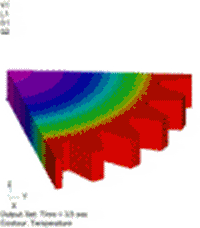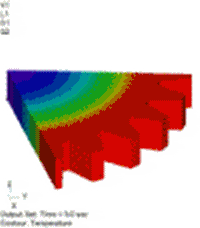図１１　温度分布[℃] 温度依存性なし（弱連成）