誘電体にマイクロ波を照射すると、誘電体は電気双極子なので、マイクロ波の周波数と同じ速さで、電場の変化に合わせて分極方向を変化させます。

この時、速い速度(高い周波数)で電界の向きを変化させると、双極子は反転する時に周囲の分子との間で摩擦を受け、電界の変化の速度に追従できなくなります。

その結果、摩擦によるエネルギーが誘電体内部で消費され、それが誘電体内部で熱に変わります(誘電損失)。

　　

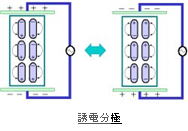
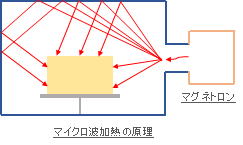
この誘電発熱が起こる原理を技術的な観点から簡単に説明します。
図１ような簡単な誘電加熱モデルを想定し、交流電圧 [ E ] を印可すると、理想的な誘電体では、[ I = Ｅ× 2πfＣ ] の電流[I]が流れ、電流[I]の位相は電圧 [ E ] に対して [ 90 ] 度進みます(図２)。

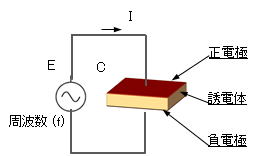図１

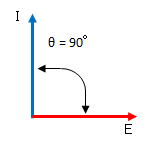図２

しかし、実際の誘電体に高周波電流を印可するとロスが発生し、電流は [δ] だけ遅れ、図３のように [ θ ] だけしか進むことができず、電圧 [ E ] と同位相の電流[ IR ]が発生します。
この[ IR ]は、[ P = IR x E]の発熱作用を発生させます。
この時の電流位相の遅れ角[δ]は誘電損失角、[ tanδ = IR/IC = 1/2πfCR ] は誘電正接 ( タンデルタ/Tanδ ) と呼ばれ、誘電体はそれぞれ固有の値を持っています。
この図３の状態を等価回路で表わすと図４のようになります。

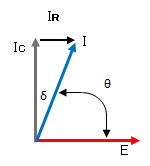図３

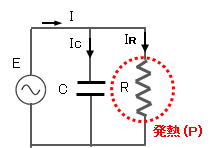図４

ここで、図１の誘電体の比誘電率[ε_r]、電極の面積[ S (m²)]、電極の間隔 [ d (m)]、周波数 [ f (Hz) ]、電圧 [ E (V) ]とすると、この誘電体モデルの静電容量 [ C ] は、C = (ε₀ x ε_r x S )/d となります。
発熱量 P は [ P = IR x E = E²/R ]、また、 [ tanδ = IR /IC = 1/2πfCR ] が成り立っていますので、P = E²/R = E² x tanδx 2πfC = E² x tanδx 2πf x (ε₀ x ε_rx S )/dとなり、発熱量 P は、電圧 ( E ) の２乗、tanδ、周波数 [ f ]、誘電体の比誘電率 [εr ]に比例することがわかります。

マイクロ波加熱解析はこちらへ