変位電流は、電界が時間的に変化することで生じる電流です。
ここで角速度を[ ω ]、周波数を[ f ] とすると、

となります。
また、誘電率εの誘電体に電場Eが存在した場合、電束Dが次の式により表されます。

電束Dは印加された電界Eにより誘電体の分極が向きをそろえる結果現れるので、電界の極性変化が速い場合はDの変化はEの変化から遅れます。
変位電流の角周波数をω、電界Eの振幅をE ₀とすると、

Dの遅れを位相 δ で表すと、

Dの時間微分が誘電体中の変位電流として、一般の電流と同等の扱いができるとし、変位電流をJ_Dとすると、

J_DとEの各実数部の積の平均値が誘電体単位体積当たりの発生電力、すなわち損失P_Lなので、

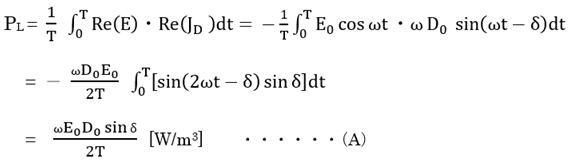
一方、DとEの比をとると、D = εEなので、

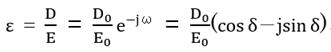
このようにDとEに位相差があると ε は複素数となる。上記式を

と書き表すと、

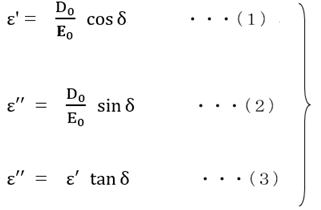
上記（２）式を用いて式（A）の右辺を書き直すと

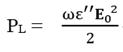
したがって、誘電体損失[ P_L ]は複素誘電率の虚部 ε''と電界Eの振幅E ₀に比例することがわかります。

※各商標または商品名はそれぞれの所有権保持者の商標または登録商標です。