高周波誘電加熱連成解析

( 誘電体内に金属線 )

高周波誘電発熱は、交番電極間に誘電体が存在すると、誘電体を構成する各分子は回転・衝突・振動・摩擦などの 激しい運動が生じ、誘電体に誘電体損失(tanδ (タンデルタ))が発生し、内部が発熱します。

誘電加熱の原理はこちらへ

この誘電体の内部に金属線(導体)含まれている場合、その金属線の周囲の温度分布がどのように変化するのか、評価解析を行ないました。

電極間に生じている電界中に導体が存在すると、導体は浮き導体となり、電位は不明ですが、全体が同電位になります。
したがってその導体の近傍だけ、発熱分布/温度分布が周囲と異なる状態になります。

この状態を、誘電加熱連成解析ソフトウェア[ F-VOLT-DH ]で解析しました。
最初に周波数応答解析機能で、電界分布と発熱密度分布を計算しました。
引き続き熱伝導連成解析を行ない、その発熱分布から時間的に変化する温度分布を過渡応答解析で求めました。

金属線(浮き導体)を誘電体内部に含む今回の解析モデルは下図の通りです。

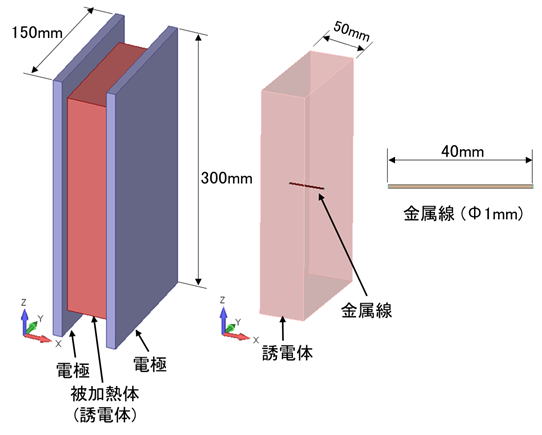
電極には交番電圧[ 6k(v) ]と[ 0(v) ] を印加し、周波数は[ 15MHz ]で計算しました。

最初に金属線を下図のように設置してみました。
金属線は、正面( ZX面 )から見ると点に見えますが、上面から見ると電極に平行に、側面から見ると水平に見える状態です。

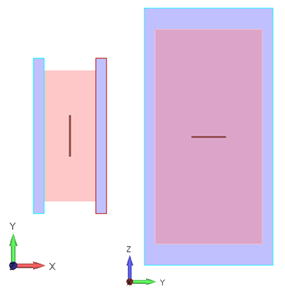
ケース [１] ：電極板に平行/水平

この場合の電界分布は次の様になりました。

電界分布コンター図 (単位：V/m) ( モデル全体 )	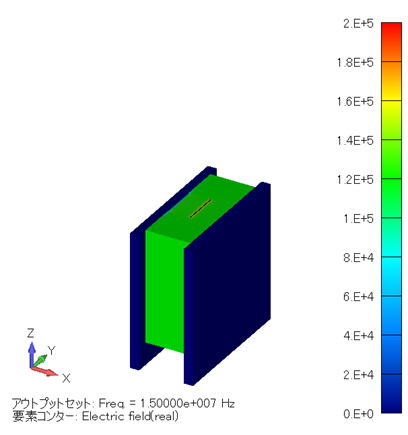電界分布コンター図 (単位：V/m) ( ＸＹ断面 )
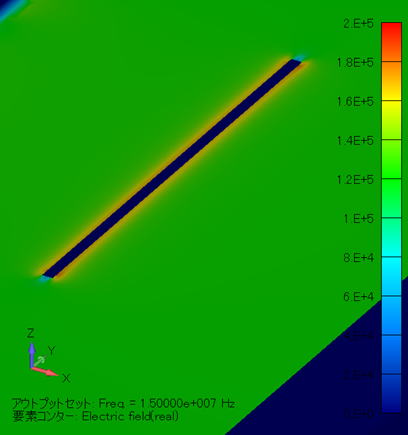電界分布コンター図 (単位：V/m) ( ＸＹ断面拡大図/金属線表示 )	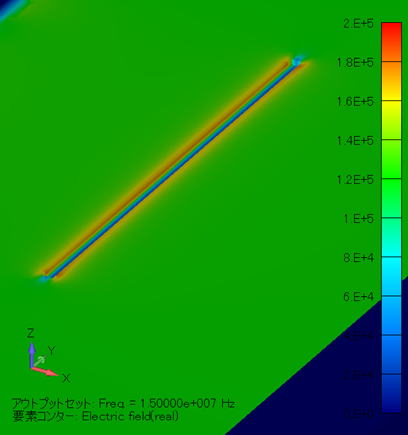電界分布コンター図 (単位：V/m) ( ＸＹ断面拡大図/金属線非表示 )

発熱密度分布は次の様になりました。

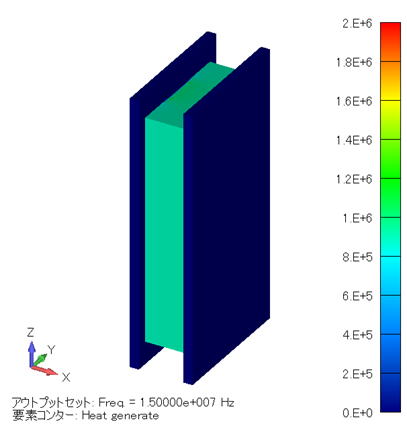発熱密度分布コンター図 (単位：W/m3) (モデル全体 )	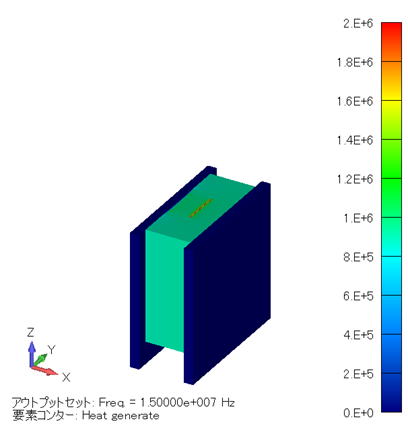発熱密度分布コンター図 (単位：W/m3) ( ＸＹ断面 )
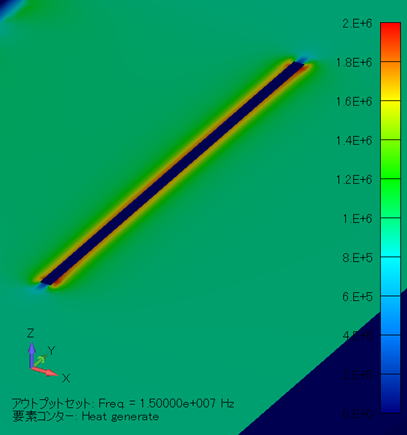発熱密度分布コンター図 (単位：W/m3) ( ＸＹ断面拡大図/金属線表示 )	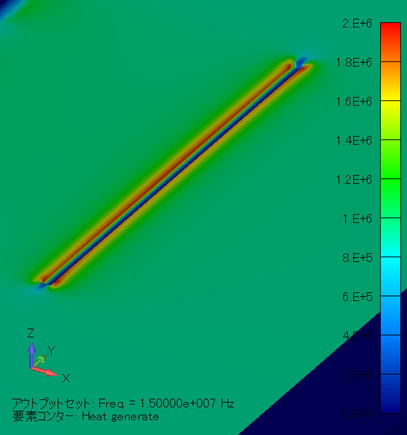発熱密度分布コンター図 (単位：W/m3) ( ＸＹ断面拡大図/金属線非表示 )

次に、金属線を下図のように電極板に垂直に設置してみました。

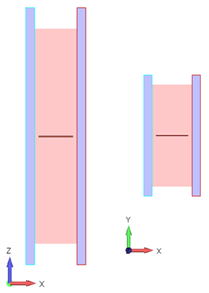
ケース [２] ： 電極板に垂直

この場合の電界分布は次の様になりました。

電界分布コンター図 (単位：V/m) ( モデル全体 )	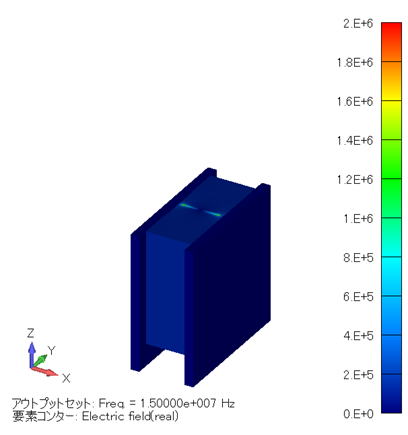電界分布コンター図 (単位：V/m) ( ＸＹ断面 )
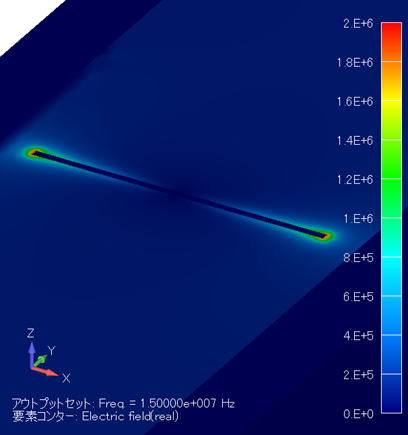電界分布コンター図 (単位：V/m) ( ＸＹ断面拡大図/金属線表示 )	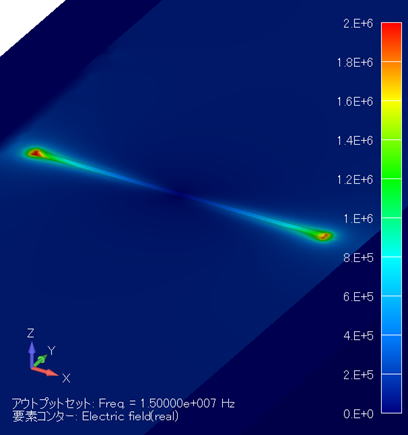電界分布コンター図 (単位：V/m) ( ＸＹ断面拡大図/金属線非表示 )

この場合の電界分布は、「 ケース [１] ：電極板に平行/水平 」の場合よりも、[10倍]高くなっています。
これは、電界強度が導体間の距離が短いほど強くなることに依存します。
数式で表すと、電界強度（ E ）は、電位差（ V ）を導体間の距離（ d ）で割ったものになります ( E = V/d )。
つまり、電位差が同じ場合、導体間の距離（ d ）が短くなるほど電界強度( E )が大きくなります。
したがって今回も、電極間の距離よりも電極と金属線の間の距離が短くなったので、電界強度( E )がその分高くなりました。

発熱密度分布は次の様になりました。

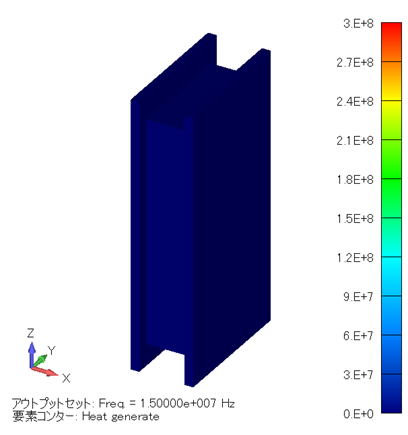発熱密度分布コンター図 (単位：W/m3)( モデル全体 )	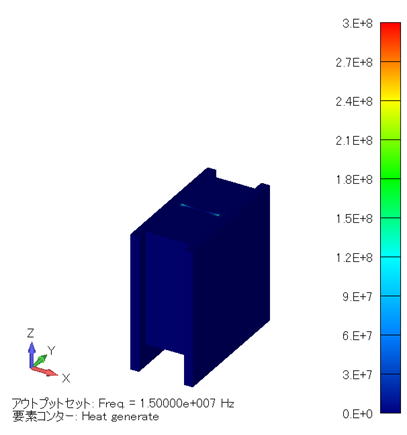発熱密度分布コンター図 (単位：W/m3)( ＸＹ断面 )
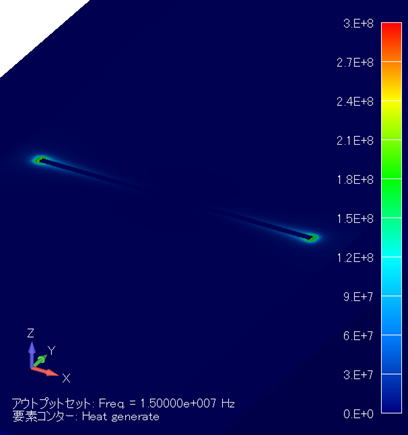発熱密度分布コンター図 (単位：W/m3) ( ＸＹ断面拡大図/金属線表示 )	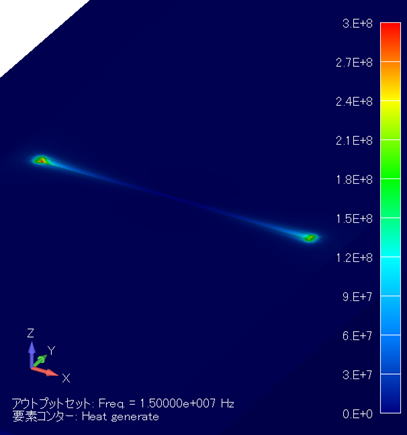発熱密度分布コンター図 (単位：W/m3) ( ＸＹ断面拡大図/金属線非表示 )

電極間に金属線が存在することにより、導体間の距離が短くなり、電界強度が高まった分、発熱密度も高まることがわかります。

３ケース目として、金属線を下図のように電極板に平行に設置してみました。
金属線は、正面から見ても側面から見ても、垂直に見える状態です。

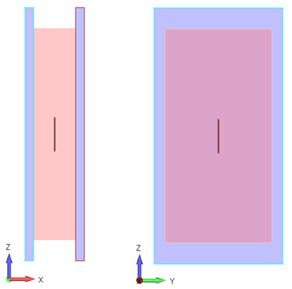
ケース [３] ：電極板に平行/垂直

この場合の電界分布は次の様になりました。

電界分布コンター図 (単位：V/m) ( モデル全体 )	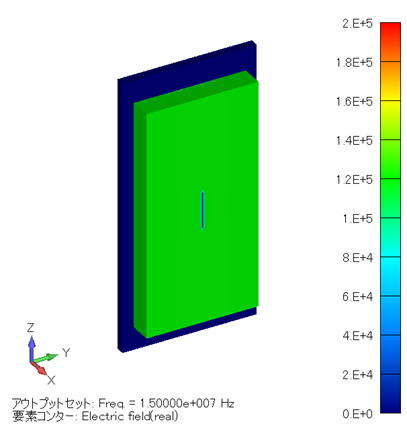電界分布コンター図 (単位：V/m) ( ＹＺ断面 )
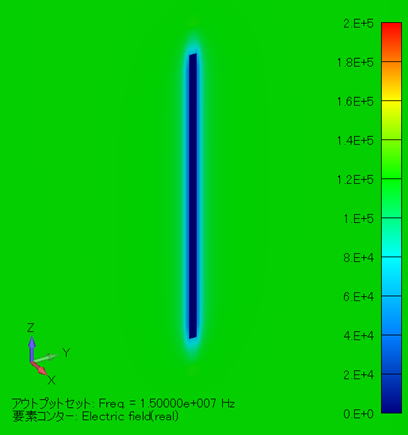電界分布コンター図 (単位：V/m) ( ＹＺ断面拡大図/金属線表示 )	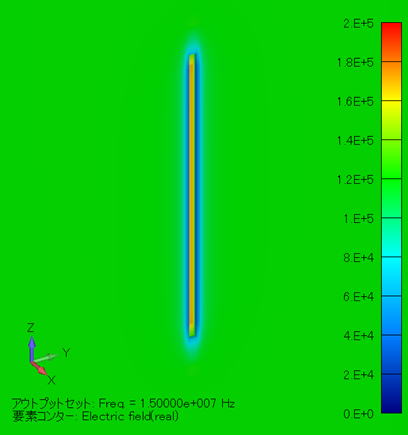電界分布コンター図 (単位：V/m) ( ＹＺ断面拡大図/金属線非表示 )

この場合、電極と金属線の間の距離がケース [１] と同じようになりますので、電界分布も、「 ケース [１] と同じような分布になります。

発熱密度分布は次の様になりました。

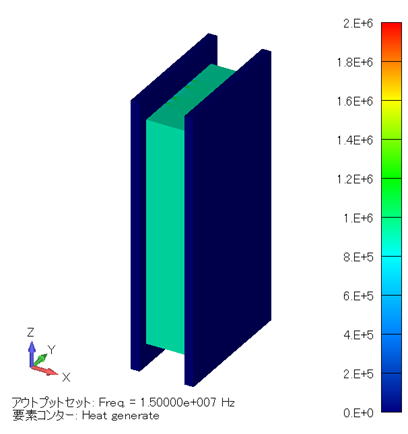発熱密度分布コンター図 (単位：W/m3) ( モデル全体 )	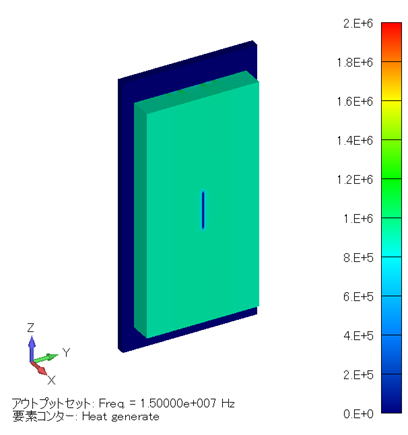発熱密度分布コンター図 (単位：W/m3) ( ＹＺ断面 )
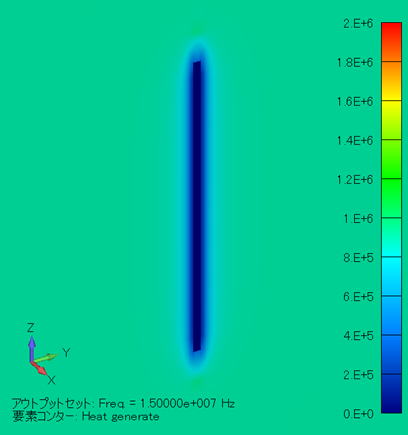発熱密度分布コンター図 (単位：W/m3) ( ＹＺ断面拡大図/金属線表示 )	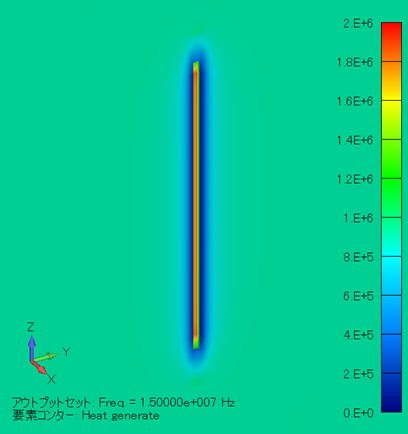発熱密度分布コンター図 (単位：W/m3) ( ＹＺ断面拡大図/金属線非表示 )

電界分布と同様に、発熱密度分布も「 ケース [１] と同じようになります。

誘電発熱が起こる原理につきましては、こちらへ。

ここでそれぞれの物性値を、熱伝導率、比熱、質量密度に変更し、発熱密度分布から時間とともに温度分布がどのように変化するか解析しました。

[ F-VOLT-DH ]は、物体表面の自然対流による放熱を考慮できますので、解析対象物表面の放熱現象を正確に計算できます。
したがって、時間とともに変化する解析対象物全体の正確な温度変化を解析することができます。
下のグラフは解析対象物の表面の自然対流境界条件で、上面、下面、側面の温度と熱伝達率の関係を示しており、温度依存性を考慮できます。

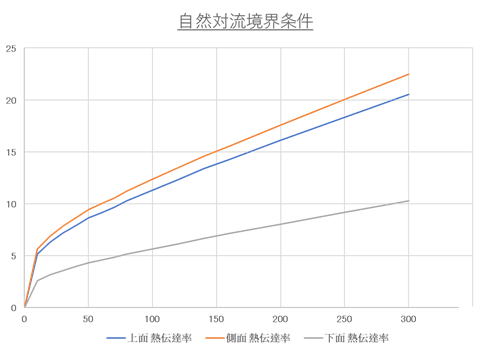
今回は評価解析ですので、上図の中から「上面の熱伝達率」をモデルの全周に設定しました。

誘電体の内部に金属線が含まれている場合、電界分布、発熱密度分布と同じように、以下の3ケースで温度分布を計算しました。

ケース [１] ：電極板に平行/水平

この場合の温度分布は次の様になりました。

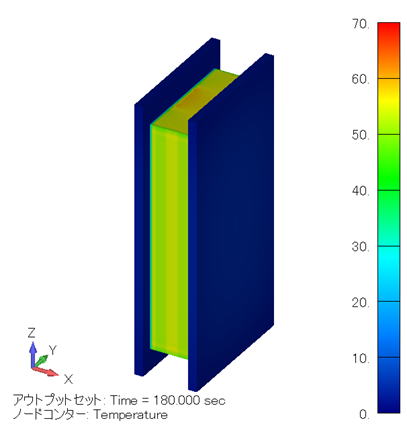温度分布コンター図 (単位：℃) ( モデル全体 )	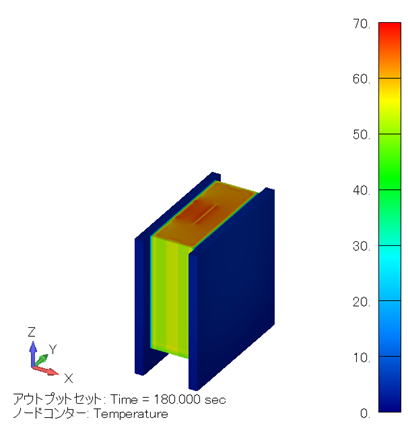温度分布コンター図 (単位：℃) ( ＸＹ断面 )
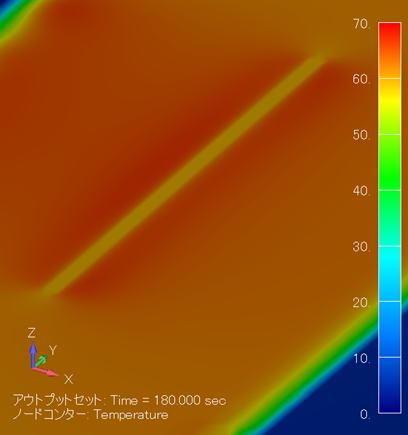温度分布コンター図 (単位：℃) ( ＸＹ断面拡大図/金属線表示 )	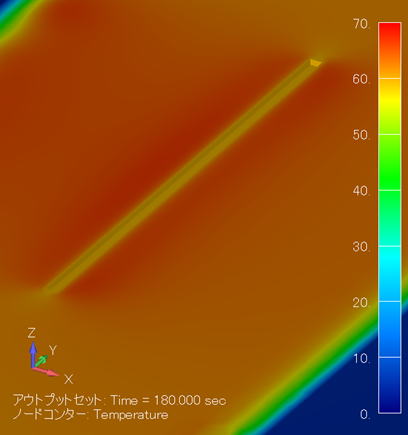温度分布コンター図 (単位：℃) ( ＸＹ断面拡大図/金属線非表示 )

このケースでは発熱密度値が小さいので、3分で70℃しか昇温しません。

次に、金属線を電極板に垂直にしたケースで温度分布を計算しました。

ケース [２] ： 電極板に垂直

この場合の温度分布は次の様になりました。

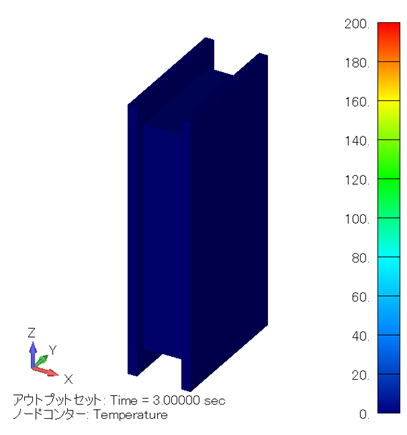温度分布コンター図 (単位：℃) ( モデル全体 )	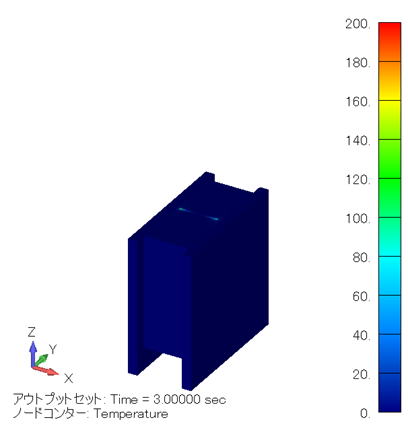温度分布コンター図 (単位：℃) ( ＸＹ断面 )
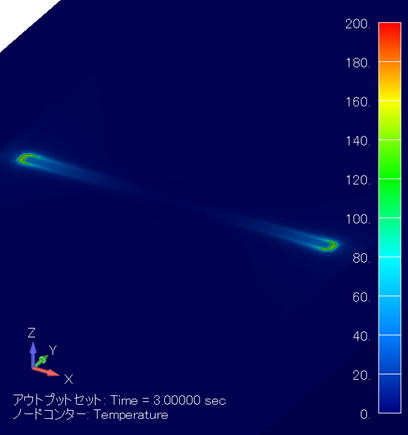温度分布コンター図 (単位：℃) ( ＸＹ断面拡大図/金属線表示 )	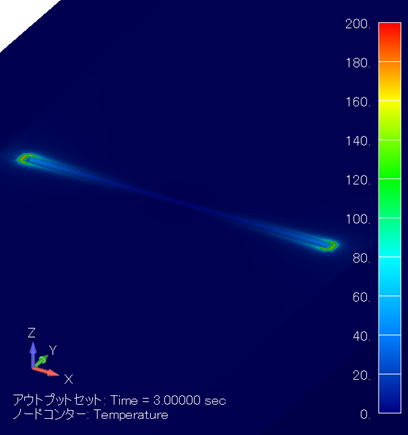温度分布コンター図 (単位：℃) ( ＸＹ断面拡大図/金属線非表示 )

このケースでは金属線が電極に最も接近しているので、その分導体間の距離が短くなることで電界強度が高まり、その分発熱密度も高まり、わずか3秒で200℃近くまで昇温していることがわかります。

３ケース目として、金属線を電極板に平行に設置した場合の温度分布を計算しました。

ケース [３] ：電極板に平行/垂直

この場合の温度分布は次の様になりました。

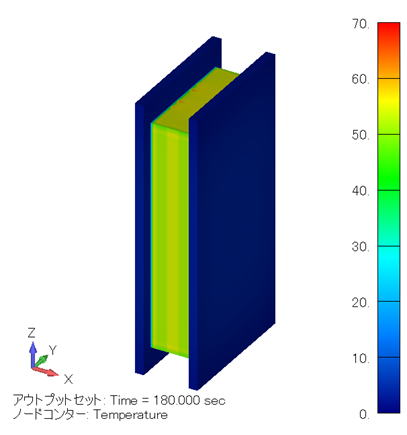温度分布コンター図 (単位：℃) ( モデル全体 )	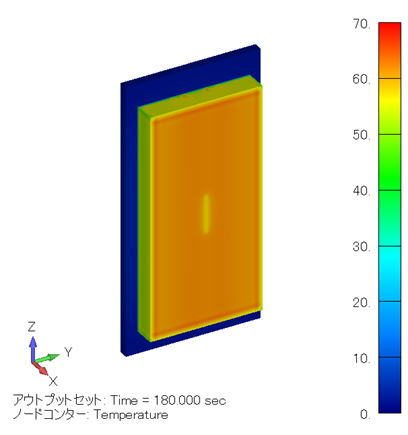温度分布コンター図 (単位：℃) ( ＹＺ断面 )
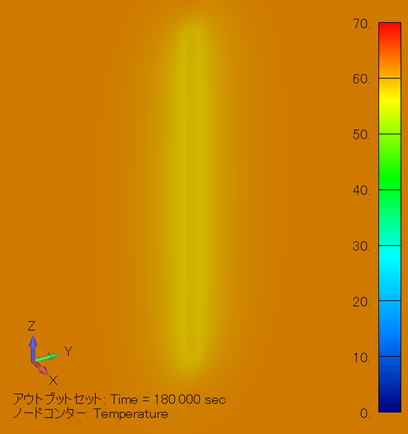温度分布コンター図 (単位：℃) ( ＹＺ断面拡大図/金属線表示 )	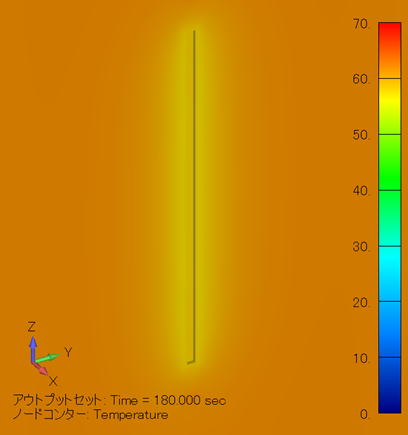温度分布コンター図 (単位：℃) ( ＹＺ断面拡大図/金属線非表示 )

この場合、電極と金属線の間の距離がケース [１] と同じようになりますので、温度分布も「 ケース [１] と同じような結果になります。

以上の結果から、電極と誘電体中の金属が接近すると、近傍の電界値と発熱密度値が大きくなり、 かなりのレベルで昇温することがわかります。

この評価解析は誘電加熱連成解析ソフトウェア F-VOLT-DH で行いました。

F-VOLT-DH につきましてこちらへ

評価解析につきましてこちらへ

ご不明な点がありましたら、お問い合わせページの「ご質問／ご要望等」欄にご記入ください。

※各商標または商品名はそれぞれの所有権保持者の商標または登録商標です。